Construction, traitement et affichage de matrices¶

Définition :¶

En mathématiques, une matrice $\textbf{M}(m \times n)$ est un tableau de nombres possédant $m$ lignes et $n$ colonnes. Chaque élément de ce tableau est repéré par deux indices i et j tel que :

Source wikipédia

Création de matrices au format de l'afficheur d'un BBC micro:bit :¶
On peut représenter les 25 LEDs de l'écran d'un BBC micro:bit par une matrice carrée (5x5) pour laquelle chaque élément peut prendre une valeur entière comprise entre 0 et 9. Cette valeur représente la luminosité de la LED correspondante.

Par exemple, l'affichage d'un "smiley happy" :

Image du simulateur TigerJython
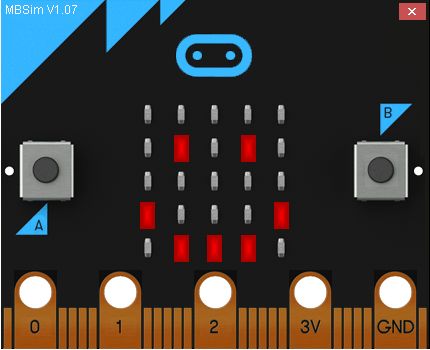
correspond à la matrice : $$joyeux =\begin{pmatrix} & 0 & 0 & 0 & 0 & 0 & \\ & 0 & 9 & 0 & 9 & 0 & \\ & 0 & 0 & 0 & 0 & 0 & \\ & 9 & 0 & 0 & 0 & 9 & \\ & 0 & 9 & 9 & 9 & 0 & \\ \end{pmatrix}$$

et au tableau définit en Python tel que :

In [20]:

joyeux = [[0, 0, 0, 0, 0], [0, 9, 0, 9, 0], [0, 0, 0, 0, 0], [9, 0, 0, 0, 9], [0, 9, 9, 9, 0]] joyeux

joyeux = [[0, 0, 0, 0, 0], [0, 9, 0, 9, 0], [0, 0, 0, 0, 0], [9, 0, 0, 0, 9], [0, 9, 9, 9, 0]] joyeux

Out[20]:

[[0, 0, 0, 0, 0], [0, 9, 0, 9, 0], [0, 0, 0, 0, 0], [9, 0, 0, 0, 9], [0, 9, 9, 9, 0]]

A coder vous même :
Définir le tableau pour l'affichage d'un "smiley sad" :

In [19]:

triste = [[0, 0, 0, 0, 0], [0, 9, 0, 9, 0], [0, 0, 0, 0, 0], [0, 9, 9, 9, 0], [9, 0, 0, 0, 9]] triste

triste = [[0, 0, 0, 0, 0], [0, 9, 0, 9, 0], [0, 0, 0, 0, 0], [0, 9, 9, 9, 0], [9, 0, 0, 0, 9]] triste

Out[19]:

[[0, 0, 0, 0, 0], [0, 9, 0, 9, 0], [0, 0, 0, 0, 0], [0, 9, 9, 9, 0], [9, 0, 0, 0, 9]]

Afficher une matrice :¶
Affichage en $\LaTeX{}$ dans ce notebook jupyter :¶
La fonction print() génère un affichage en ligne d'un tableau et non pas un format matricielle, lignes/colonnes :

In [21]:

print(joyeux)

print(joyeux)

[[0, 0, 0, 0, 0], [0, 9, 0, 9, 0], [0, 0, 0, 0, 0], [9, 0, 0, 0, 9], [0, 9, 9, 9, 0]]

Pour afficher comme il se doit nos matrices dans ce document, nous allons définir une fonction basée sur la fonction Latex() du module IPython.display

A faire vous même :
Essayer la fonction suivante avec les matrices joyeux puis triste.

In [22]:

from IPython.display import Latex def affiche_latex(matrice) : ''' ################################################### # # # cette fonction prend en entrée un tableau. # # et ressort le même tableau dans des paranthèses # # # ################################################### ''' S = '$$\\begin{pmatrix}' for i in range(len(matrice)) : S += '&' for j in range(len(matrice[i])) : S += f' {matrice[i][j]} &' S +=" \\\\" S +='\\end{pmatrix}$$' return Latex(S)

from IPython.display import Latex def affiche_latex(matrice) : ''' ################################################### # # # cette fonction prend en entrée un tableau. # # et ressort le même tableau dans des paranthèses # # # ################################################### ''' S = '$$\\begin{pmatrix}' for i in range(len(matrice)) : S += '&' for j in range(len(matrice[i])) : S += f' {matrice[i][j]} &' S +=" \\\\" S +='\\end{pmatrix}$$' return Latex(S)

In [23]:

from IPython.display import Latex def affiche_latex(matrice) : ''' ################################################### # # # cette fonction prend en entrée un tableau. # # et ressort le même tableau dans des paranthèses # # # ################################################### ''' S = '$$\\begin{pmatrix}' for i in range(len(matrice)) : S += '&' for j in range(len(matrice[i])) : S += f' {matrice[i][j]} &' S +=" \\\\" S +='\\end{pmatrix}$$' return S affiche_latex(joyeux)

from IPython.display import Latex def affiche_latex(matrice) : ''' ################################################### # # # cette fonction prend en entrée un tableau. # # et ressort le même tableau dans des paranthèses # # # ################################################### ''' S = '$$\\begin{pmatrix}' for i in range(len(matrice)) : S += '&' for j in range(len(matrice[i])) : S += f' {matrice[i][j]} &' S +=" \\\\" S +='\\end{pmatrix}$$' return S affiche_latex(joyeux)

Out[23]:

'$$\\begin{pmatrix}& 0 & 0 & 0 & 0 & 0 & \\\\& 0 & 9 & 0 & 9 & 0 & \\\\& 0 & 0 & 0 & 0 & 0 & \\\\& 9 & 0 & 0 & 0 & 9 & \\\\& 0 & 9 & 9 & 9 & 0 & \\\\\\end{pmatrix}$$'

In [24]:

affiche_latex(joyeux)

affiche_latex(joyeux)

Out[24]:

'$$\\begin{pmatrix}& 0 & 0 & 0 & 0 & 0 & \\\\& 0 & 9 & 0 & 9 & 0 & \\\\& 0 & 0 & 0 & 0 & 0 & \\\\& 9 & 0 & 0 & 0 & 9 & \\\\& 0 & 9 & 9 & 9 & 0 & \\\\\\end{pmatrix}$$'

In [25]:

affiche_latex(triste)

affiche_latex(triste)

Out[25]:

'$$\\begin{pmatrix}& 0 & 0 & 0 & 0 & 0 & \\\\& 0 & 9 & 0 & 9 & 0 & \\\\& 0 & 0 & 0 & 0 & 0 & \\\\& 0 & 9 & 9 & 9 & 0 & \\\\& 9 & 0 & 0 & 0 & 9 & \\\\\\end{pmatrix}$$'

Que fait la fonction affiche_latex()? Rédiger une docstring pour cette fonction...

In [26]:

help(affiche_latex)

help(affiche_latex)

Help on function affiche_latex in module __main__: affiche_latex(matrice) ################################################### # # # cette fonction prend en entrée un tableau. # # et ressort le même tableau dans des paranthèses # # # ###################################################

Affichage sur l'écran d'un BBC micro:bit :¶
La fonction: display.set_pixel(x,y,n) permet d’allumer la LED de la colonne x (nombre entier entre 0 et 4) et de la ligne y (nombre entier entre 0 et 4) avec un niveau d'intensité lumineuse n (nombre entier entre 0 et 9).

Exemple: display.set_pixel(1,2,7) allume la LED située à la colonne 1 de la ligne 2 au niveau d'intensité lumineuse 7.

Guide pour matrice à LED

A coder vous même :
Dans le programme suivant, définir une fonction affiche_microbit(matrice) qui :

prend en paramètre une matrice (5x5) dont les éléments sont des nombres entiers compris entre 0 et 9 ;

parcourt cette matrice par ligne et par colonne avec deux boucles for imbriquées ;

lit la valeur de chaque élément et l'affecte au pixel (LED) correspondant sur l'écran du BBC micro:bit.

Tester votre programme sur simulateur et sur BBC micro:bit pour les matrices joyeux et triste.

In [27]:

from microbit import * joyeux = [[0, 0, 0, 0, 0], [0, 9, 0, 9, 0], [0, 0, 0, 0, 0], [9, 0, 0, 0, 9], [0, 9, 9, 9, 0]] def affiche_microbit(matrice) : ''' ################################################ # # # Documentation de la fonction ........... # # # ################################################ ''' for i for j affiche_microbit(joyeux)

from microbit import * joyeux = [[0, 0, 0, 0, 0], [0, 9, 0, 9, 0], [0, 0, 0, 0, 0], [9, 0, 0, 0, 9], [0, 9, 9, 9, 0]] def affiche_microbit(matrice) : ''' ################################################ # # # Documentation de la fonction ........... # # # ################################################ ''' for i for j affiche_microbit(joyeux)

File "<ipython-input-27-7ddd7df63584>", line 18 for i ^ SyntaxError: invalid syntax

Prolongement :

Modifier le programme pour afficher alternativement les images joyeux puis triste ;

Redéfinir une fonction affiche_microbit(matrice) utilisant la classe Image et la fonction display.show() :

In [28]:

monImage = Image('33333:36663:36963:36663:33333:') display.show(monImage)

monImage = Image('33333:36663:36963:36663:33333:') display.show(monImage)

--------------------------------------------------------------------------- NameError Traceback (most recent call last) <ipython-input-28-603f645ad225> in <module> ----> 1 monImage = Image('33333:36663:36963:36663:33333:') 2 display.show(monImage) NameError: name 'Image' is not defined

Affichage sur une grille IPythonBlocks dans ce notebook jupyter :¶
Instructions de base pour l'utilisation du module IPythonBlocks :

In [29]:

# On importe la fonction BlockGrid() du module ipythonblocks from ipythonblocks import BlockGrid # On crée un objet maGrille, une instance de BlockGrid maGrille = BlockGrid(8,5, fill=(0, 0, 0), block_size=40) # On accède à chaque case de la grille par ces index [i,j] pour modifier sa couleur (rouge, vert, bleu) maGrille[2,3]=(255, 0, 0) # On affiche notre grille maGrille

# On importe la fonction BlockGrid() du module ipythonblocks from ipythonblocks import BlockGrid # On crée un objet maGrille, une instance de BlockGrid maGrille = BlockGrid(8,5, fill=(0, 0, 0), block_size=40) # On accède à chaque case de la grille par ces index [i,j] pour modifier sa couleur (rouge, vert, bleu) maGrille[2,3]=(255, 0, 0) # On affiche notre grille maGrille

Out[29]:

A coder vous même :
Dans le programme suivant, définir une fonction affiche_ipythonblocks(matrice) qui :

prend en paramètre une matrice (5x5) dont les éléments sont des nombres entiers compris entre 0 et 9 ;

parcourt cette matrice par ligne et par colonne avec deux boucles for imbriquées ;

lit la valeur de chaque élément et l'adapte à la couleur de la case correspondante dans une grille ipythonblocks (5x5).

Tester votre programme dans ce notebook pour les matrices joyeux et triste.

In [30]:

from ipythonblocks import BlockGrid def affiche_ipythonblocks(matrice) : ''' ################################################ # # # Documentation de la fonction ........... # # # ################################################ ''' maGrille = BlockGrid(5,5, fill=(0, 0, 0), block_size=30) for i in range(len(matrice)) : for j in range(len(matrice[i])) : maGrille[i,j]=(matrice[i][j]*255/9, 0, 0) return maGrille

from ipythonblocks import BlockGrid def affiche_ipythonblocks(matrice) : ''' ################################################ # # # Documentation de la fonction ........... # # # ################################################ ''' maGrille = BlockGrid(5,5, fill=(0, 0, 0), block_size=30) for i in range(len(matrice)) : for j in range(len(matrice[i])) : maGrille[i,j]=(matrice[i][j]*255/9, 0, 0) return maGrille

In [31]:

affiche_ipythonblocks(joyeux)

affiche_ipythonblocks(joyeux)

Out[31]:

In [32]:

affiche_ipythonblocks(triste)

affiche_ipythonblocks(triste)

Out[32]:

Création de matrices par compréhension :¶
Déclarer une matrice élément par élément peux être fastidieux.

La compréhension de liste va nous permettre d'automatiser cette tâche.

A programmer vous même :
En vous inspirant de l'exemple suivant :

In [33]:

moins = [[0 if i != 2 else 9 for j in range(5)] for i in range(5)] moins

moins = [[0 if i != 2 else 9 for j in range(5)] for i in range(5)] moins

Out[33]:

[[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [9, 9, 9, 9, 9], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]]

In [34]:

affiche_latex(moins)

affiche_latex(moins)

Out[34]:

'$$\\begin{pmatrix}& 0 & 0 & 0 & 0 & 0 & \\\\& 0 & 0 & 0 & 0 & 0 & \\\\& 9 & 9 & 9 & 9 & 9 & \\\\& 0 & 0 & 0 & 0 & 0 & \\\\& 0 & 0 & 0 & 0 & 0 & \\\\\\end{pmatrix}$$'

In [35]:

affiche_ipythonblocks(moins)

affiche_ipythonblocks(moins)

Out[35]:

Proposer des solutions pour générer par compréhension les matrices telles que :
$$plein\_feux = \begin{pmatrix} & 9 & 9 & 9 & 9 & 9 & \\ & 9 & 9 & 9 & 9 & 9 & \\ & 9 & 9 & 9 & 9 & 9 & \\ & 9 & 9 & 9 & 9 & 9 & \\ & 9 & 9 & 9 & 9 & 9 & \\ \end{pmatrix}$$

In [38]:

plein_feux = [[9 if i != 2 else 9 for j in range(5)] for i in range(5)]

plein_feux = [[9 if i != 2 else 9 for j in range(5)] for i in range(5)]

In [39]:

affiche_latex(plein_feux)

affiche_latex(plein_feux)

Out[39]:

'$$\\begin{pmatrix}& 9 & 9 & 9 & 9 & 9 & \\\\& 9 & 9 & 9 & 9 & 9 & \\\\& 9 & 9 & 9 & 9 & 9 & \\\\& 9 & 9 & 9 & 9 & 9 & \\\\& 9 & 9 & 9 & 9 & 9 & \\\\\\end{pmatrix}$$'

In [40]:

affiche_ipythonblocks(plein_feux)

affiche_ipythonblocks(plein_feux)

Out[40]:

$$plus = \begin{pmatrix} & 0 & 0 & 9 & 0 & 0 & \\ & 0 & 0 & 9 & 0 & 0 & \\ & 9 & 9 & 9 & 9 & 9 & \\ & 0 & 0 & 9 & 0 & 0 & \\ & 0 & 0 & 9 & 0 & 0 & \\ \end{pmatrix}$$

In [147]:

plus = [[0 if i != 2 and j != 2 else 9 for j in range(5)] for i in range(5)]

plus = [[0 if i != 2 and j != 2 else 9 for j in range(5)] for i in range(5)]

In [148]:

affiche_latex(plus)

affiche_latex(plus)

Out[148]:

'$$\\begin{pmatrix}& 0 & 0 & 9 & 0 & 0 & \\\\& 0 & 0 & 9 & 0 & 0 & \\\\& 9 & 9 & 9 & 9 & 9 & \\\\& 0 & 0 & 9 & 0 & 0 & \\\\& 0 & 0 & 9 & 0 & 0 & \\\\\\end{pmatrix}$$'

In [149]:

affiche_ipythonblocks(plus)

affiche_ipythonblocks(plus)

Out[149]:

$$fois = \begin{pmatrix} & 9 & 0 & 0 & 0 & 9 & \\ & 0 & 9 & 0 & 9 & 0 & \\ & 0 & 0 & 9 & 0 & 0 & \\ & 0 & 9 & 0 & 9 & 0 & \\ & 9 & 0 & 0 & 0 & 9 & \\ \end{pmatrix}$$

In [208]:

fois = [[9 if i==j or i + j == 4 else 0 for j in range(5)] for i in range(5)]

fois = [[9 if i==j or i + j == 4 else 0 for j in range(5)] for i in range(5)]

In [209]:

affiche_latex(fois)

affiche_latex(fois)

Out[209]:

'$$\\begin{pmatrix}& 9 & 0 & 0 & 0 & 9 & \\\\& 0 & 9 & 0 & 9 & 0 & \\\\& 0 & 0 & 9 & 0 & 0 & \\\\& 0 & 9 & 0 & 9 & 0 & \\\\& 9 & 0 & 0 & 0 & 9 & \\\\\\end{pmatrix}$$'

In [210]:

affiche_ipythonblocks(fois)

affiche_ipythonblocks(fois)

Out[210]:

$$ degrade\_Est = \begin{pmatrix} & 1 & 3 & 5 & 7 & 9 & \\ & 1 & 3 & 5 & 7 & 9 & \\ & 1 & 3 & 5 & 7 & 9 & \\ & 1 & 3 & 5 & 7 & 9 & \\ & 1 & 3 & 5 & 7 & 9 & \\ \end{pmatrix}$$

In [253]:

degrade_Est = [[1 if j ==0 else j + 2 for j in range(5)] for i in range(5)]

degrade_Est = [[1 if j ==0 else j + 2 for j in range(5)] for i in range(5)]

In [254]:

affiche_latex(degrade_Est)

affiche_latex(degrade_Est)

Out[254]:

'$$\\begin{pmatrix}& 1 & 3 & 4 & 5 & 6 & \\\\& 1 & 3 & 4 & 5 & 6 & \\\\& 1 & 3 & 4 & 5 & 6 & \\\\& 1 & 3 & 4 & 5 & 6 & \\\\& 1 & 3 & 4 & 5 & 6 & \\\\\\end{pmatrix}$$'

In [255]:

affiche_ipythonblocks(degrade_Est)

affiche_ipythonblocks(degrade_Est)

Out[255]:

$$ degrade\_Sud\_Est = \begin{pmatrix} & 1 & 2 & 3 & 4 & 5 & \\ & 2 & 3 & 4 & 5 & 6 & \\ & 3 & 4 & 5 & 6 & 7 & \\ & 4 & 5 & 6 & 7 & 8 & \\ & 5 & 6 & 7 & 8 & 9 & \\ \end{pmatrix}$$

In [266]:

degrade_Sud_Est = [[9 if i==j or i + j == 4 else i-j==3 for j in range(5)] for i in range(5)]

degrade_Sud_Est = [[9 if i==j or i + j == 4 else i-j==3 for j in range(5)] for i in range(5)]

In [267]:

affiche_latex(degrade_Sud_Est)

affiche_latex(degrade_Sud_Est)

Out[267]:

'$$\\begin{pmatrix}& 9 & False & False & False & 9 & \\\\& False & 9 & False & 9 & False & \\\\& False & False & 9 & False & False & \\\\& True & 9 & False & 9 & False & \\\\& 9 & True & False & False & 9 & \\\\\\end{pmatrix}$$'

In [268]:

affiche_ipythonblocks(degrade_Sud_Est)

affiche_ipythonblocks(degrade_Sud_Est)

Out[268]:

Prolongement :
Imaginer d'autres matrices (5x5) et les afficher dans ce notebook...

In [ ]:

autre = []

autre = []

Quelques opérations sur les matrices¶
Addition ou Soustraction de matrices :¶
L'addition (ou la soustraction) de deux matrices de même dimension mat_A et mat_B est égale à la matrice dont chaque coefficient est obtenu en additionnant (ou en soustrayant) les coefficients de la matrice mat_A au coefficient correspondant de la matrice mat_B.

Exemple :
$$ \begin{pmatrix} 1 & 2 & 0 \\ 4 & 3 & -1 \\ \end{pmatrix} + \begin{pmatrix} 5 & 2 & 3 \\ 1 & 3 & 4 \\ \end{pmatrix} =\begin{pmatrix} 6 & 4 & 3 \\ 5 & 6 & 3 \\ \end{pmatrix}$$
A faire vous même :
Vérifier cet exemple et documenter la fonction addition(mat_A, mat_B) du script suivant :

In [ ]:

def addition(mat_A, mat_B) : ''' ################################################ # # # Documentation de la fonction ........... # # # ################################################ ''' return [[(mat_A[i][j] + mat_B[i][j]) for j in range(len(mat_A[0]))] for i in range(len(mat_A))] affiche_latex(addition([[1, 2, 0],[4, 3, -1]],[[5, 2, 3],[1, 3, 4]]))

def addition(mat_A, mat_B) : ''' ################################################ # # # Documentation de la fonction ........... # # # ################################################ ''' return [[(mat_A[i][j] + mat_B[i][j]) for j in range(len(mat_A[0]))] for i in range(len(mat_A))] affiche_latex(addition([[1, 2, 0],[4, 3, -1]],[[5, 2, 3],[1, 3, 4]]))

A programmer vous même :

Définir une fonction de soustraction de matrice ;

Afficher les matrices résultantes des opérations :

plein_feux - joyeux

plein_feux - fois

plein_feux - degrade_Est

plein_feux - degrade_Sud_Est

Comparer les images résultantes avec les images retranchées...

In [ ]:

def soustraction(mat_A, mat_B) : ''' ################################################ # # # Documentation de la fonction ........... # # # ################################################ ''' return []

def soustraction(mat_A, mat_B) : ''' ################################################ # # # Documentation de la fonction ........... # # # ################################################ ''' return []

In [ ]:

affiche_latex(soustraction(plein_feux, joyeux))

affiche_latex(soustraction(plein_feux, joyeux))

In [ ]:

affiche_ipythonblocks(soustraction(plein_feux, joyeux))

affiche_ipythonblocks(soustraction(plein_feux, joyeux))

Transposition d'une matrice :¶
La transposée $^tM$ d'une matrice $M(m\times n)$ est la matrice $(n\times m)$ obtenue en échangeant les lignes et les colonnes de la matrice $M$.

Exemple :

Pour : $M=\begin{pmatrix} 1 & 2 & 0 \\ 4 & 3 & -1 \\ \end{pmatrix}$

Alors : $^tM=\begin{pmatrix} 1 & 4 \\ 2 & 3 \\ 0 &-1 \end{pmatrix}$

A coder vous même :
Définir une fonction transpose(matrice) qui :

prend en paramètre une matrice (mxn) dont les éléments sont des nombres entiers ;

renvoie la matrice transposée (nxm).

Appliquer votre fonction pour calculer les tranposées des matrices (5x5) précédentes...

In [ ]:

def transpose(matrice) : ''' ################################################ # # # Documentation de la fonction ........... # # # ################################################ ''' return []

def transpose(matrice) : ''' ################################################ # # # Documentation de la fonction ........... # # # ################################################ ''' return []

Un peu d'animation :¶
Sur un BBC micro:bit :¶
A faire vous même :

Compléter le programme suivant en y intégrant vos développements précédents puis le tester sur simulateur et sur BBC micro:bit ;

Expliquer le calcul k % len(ecrans)

In [ ]:

from microbit import * plein_feux = [] plus = [] fois = [] def affiche_microbit(matrice) : for i for j return def soustraction(mat_A, mat_B) : return [] ecrans = [plein_feux, soustraction(plein_feux, plus), plus, soustraction(plein_feux, plein_feux), fois, soustraction(plein_feux, fois)] k = 0 while k < 100 : affiche_microbit(ecrans[k % len(ecrans)]) sleep(500) k+=1

from microbit import * plein_feux = [] plus = [] fois = [] def affiche_microbit(matrice) : for i for j return def soustraction(mat_A, mat_B) : return [] ecrans = [plein_feux, soustraction(plein_feux, plus), plus, soustraction(plein_feux, plein_feux), fois, soustraction(plein_feux, fois)] k = 0 while k < 100 : affiche_microbit(ecrans[k % len(ecrans)]) sleep(500) k+=1

Avec IpythonBlocks dans ce notebook :¶
La fonction flash() d'une instance de BlockGrid permet un affichage animé selon le paramètre de temps display_time :

In [ ]:

from ipythonblocks import BlockGrid ecrans = [plein_feux, soustraction(plein_feux, plus), plus, soustraction(plein_feux, plein_feux), fois, soustraction(plein_feux, fois)] k = 0 while k < 100 : affiche_ipythonblocks(ecrans[k % len(ecrans)]).flash(display_time=0.5) k+=1

from ipythonblocks import BlockGrid ecrans = [plein_feux, soustraction(plein_feux, plus), plus, soustraction(plein_feux, plein_feux), fois, soustraction(plein_feux, fois)] k = 0 while k < 100 : affiche_ipythonblocks(ecrans[k % len(ecrans)]).flash(display_time=0.5) k+=1

Affichage avec ipycanvas dans ce notebook jupyter :¶
Reproduire aves le module ipycanvas un affichage similaire à celui obtenu avec IPythonBlocks :

In [ ]:

from ipycanvas import Canvas def affiche_ipycanvas(matrice) : maGrille = Canvas(width=..., height=...) for i for j return maGrille

from ipycanvas import Canvas def affiche_ipycanvas(matrice) : maGrille = Canvas(width=..., height=...) for i for j return maGrille

In [ ]:

affiche_ipycanvas(joyeux)

affiche_ipycanvas(joyeux)

Prolongement :
Imaginer d'autres animations...

Développer de nouvelles matrices...

Développer de nouvelles opérations sur des matrices...

Développer d'autres fonctions d'affichage :

- Dans un notebook avec des fonctions Ipython.display comme HTML, SVG, - Pour d'autres matrices à LEDs : - Matrice 8x8 pour BBC microbit - SenseHat sur RaspberryPi - Anneau pour BBC microbit - Anneau de CPX - Anneau d'Halocode

Références aux programmes :¶

Contenus Capacités attendues Commentaires

Tableau indexé,
tableau donné en compréhension Lire et modifier les éléments d’un tableau grâce à leurs index.
Construire un tableau par compréhension.
Utiliser des tableaux de tableaux pour représenter des matrices : notation a [i] [j].
Itérer sur les éléments d’un tableau. Seuls les tableaux dont les éléments sont du même type sont présentés.
Aucune connaissance des tranches (slices) n’est exigible.
L’aspect dynamique des tableaux de Python n’est pas évoqué.
Python identifie listes et tableaux.
Il n’est pas fait référence aux tableaux de la bibliothèque NumPy.

Contenus Capacités attendues Commentaires

Spécification. Prototyper une fonction.
Décrire les préconditions sur les arguments.
Décrire des postconditions sur les résultats. Des assertions peuvent être utilisées pour garantir des préconditions ou des postconditions.

Mise au point de programmes Utiliser des jeux de tests. L’importance de la qualité et du nombre des tests est mise en évidence.
Le succès d’un jeu de tests ne garantit pas la correction d’un programme.

Utilisation de bibliothèques Utiliser la documentation d’une bibliothèque. Aucune connaissance exhaustive d’une bibliothèque particulière n’est exigible.

Ce document est mis à disposition selon les termes de la Licence Creative Commons Attribution - Partage dans les Mêmes Conditions 4.0 International.

Pour toute question, suggestion ou commentaire : eric.madec@ecmorlaix.fr

Contenus	Capacités attendues	Commentaires
Spécification.	Prototyper une fonction. Décrire les préconditions sur les arguments. Décrire des postconditions sur les résultats.	Des assertions peuvent être utilisées pour garantir des préconditions ou des postconditions.
Mise au point de programmes	Utiliser des jeux de tests.	L’importance de la qualité et du nombre des tests est mise en évidence. Le succès d’un jeu de tests ne garantit pas la correction d’un programme.
Utilisation de bibliothèques	Utiliser la documentation d’une bibliothèque.	Aucune connaissance exhaustive d’une bibliothèque particulière n’est exigible.